
graphGame
Hai người chơi A và B chơi một trò chơi trên một đồ thị vô hướng đơn giản có n đỉnh và m cạnh. Hai người sẽ thay phiên nhau chơi, người chơi A sẽ bắt đầu chơi trước. Khi tới lượt người chơi sẽ chọn một đỉnh X có bậc là một số nguyên chẵn và xóa đỉnh X cùng với các cạnh có X là đầu mút. Nếu như khi tới lượt mà người chơi không thể chọn đỉnh X nào hay là đồ thị đã xóa hết đỉnh thì người chơi đó sẽ thua.
Hỏi nếu như cả hai người chơi đều chơi tối ưu thì kết quả cuối cùng người nào sẽ thắng.
Note: Bậc của đỉnh X là số cạnh hiện tại mà X là một trong hai đầu mút
Ví dụ:
n = 3, m = 3, e = [[1, 2], [2, 3], [1, 3]] thì graphGame(n, m, e) = "A"
Giải thích: NgườiAbắt đầu trước sẽ chọn đỉnh1có bậc là 2 và xóa nó đi cùng với các cạnh(1, 2); (1, 3)đi khỏi đồ thị khi đó tới lượtBchơi thì không còn đỉnh có bậc là chẵn (đỉnh2và3lúc này đều có bậc là 1) do đó ngườiAsẽ là người thắng.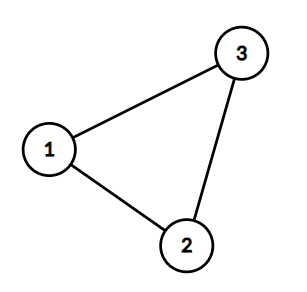
n = 3, m = 2, e = [[1, 2], [1, 3]] thì graphGame(n, m, e) = "A"
Giải thích: NgườiAsẽ chọn đỉnh1trước, thì còn lại hai đỉnh2và3đều có bậc là 0 thì người B tiếp theo chọn bất cứ đỉnh nào thì ngườiAsẽ chọn đỉnh còn lại và thắng.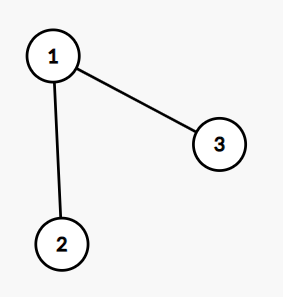
n = 4, m = 4, e = [[1, 2], [2, 3], [3, 4], [1, 4]] thì graphGame(n, m, e) = "B".
Giải thích: NgườiAchọn bất cứ đỉnh nào bắt đầu trước thì đồ thị sau khi xóa đỉnh đó cùng với các cạnh sẽ đưa về dạng ở ví dụ thứ 2. Mà ta đã biết ở vị dụ thứ 2 thì người nào bắt đầu trước sẽ chiến thắng nên cuối cùngBsẽ là người thắng.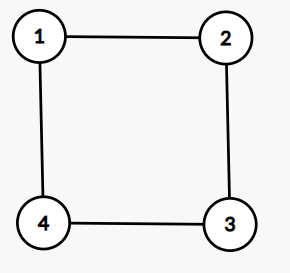
Đầu vào/Đầu ra:
- [Giới hạn thời gian chạy]: 0.5 giây với C++, 3 giây với Java và C#, 4s với Python, GO và Js.
- [Đầu vào] integer n, m
0 <= n, m <= 5000 - [Đầu vào] matrix.integer e
Danh sách các cạnh e của đồ thị
e.size() = m
e[i].size() = 2
1 <= e[i][0], e[i][1] <= n
Đảm bảo đồ thị thỏa chỉ có tối đa một cạnh nối với mọi cặp đỉnh và không có cạnh khuyên (cạnh nối dạngu-u). Đồ thị có thể không liên thông và cũng có thể là đồ thị rỗng (ban đầu không có đỉnh nào) - [Đầu ra] string
Trả về"A"nếu như người chơiAthắng và ngược lại"B"nếu như người chơiBthắng







Post Comment