
Flash Sort – Thuật Toán Sắp Xếp Thần Thánh
Bài viết sẽ làm rõ về Flash Sort – một thuật toán cho tốc độ rất nhanh trong thực tế, tuy nhiên cách thức cài đặt lại tương đối phức tạp.
Flash Sort là gì?
Nhắc tới Flash có lẽ chúng ta sẽ nghĩ đến hình ảnh này

Tuy nhiên ngày hôm nay chúng ta sẽ không nói đến The Flash, mà sẽ là 1 thuật toán có tên giống với siêu anh hùng có nguồn gốc từ DC này: Flash Sort.
Flash Sort ra đời năm 1998 bởi tác giả Karl-Dietrich Neubert, sở dĩ tác giả tự tin đặt tên là “Flash Sort” có lẽ là bởi ông rất tự tin về tốc độ chớp nhoáng của thuật toán sắp xếp này. Và trên thực tế thuật toán này cho tốc độ rất nhanh (các bạn có thể xem số 1 số thống kê nhỏ mà mình từng đề cập ở bài viết này Đâu Mới Là Thuật Toán Sắp Xếp Tốt Nhất? (codelearn.io))
Flash sort hoạt động như thế nào?
Flash sort là một thuật toán sắp xếp tại chỗ (in-situ, không dùng mảng phụ) có độ phức tạp O(n), không đệ qui, gồm có 3 bước: (1) Phân lớp dữ liệu, tức là dựa trên giả thiết dữ liệu tuân theo 1 phân bố nào đó, chẳng hạn phân bố đều, để tìm 1 công thức ước tính vị trí (lớp) của phần tử sau khi sắp xếp. (2) Hoán vị toàn cục, tức là dời chuyển các phần tử trong mảng về lớp của mình. (3) Sắp xếp cục bộ, tức là để sắp xếp lại các phần tử trong phạm vi của từng lớp.
Quá trình này cũng tương tự như việc xếp lớp và xếp chỗ cho học sinh lớp 1 trong một trường học, theo tên học sinh. (Giả sử tên học sinh được phân bố đều; thực tế điều này không đúng, chẳng hạn, số tên vần H, T thường nhiều hơn vần A, B, C.)
Lúc đầu các học sinh đang ngồi trong các phòng học của trường, nhưng không theo thứ tự nào cả.
(1) Phân lớp: 26 phòng học mỗi phòng sẽ là 1 lớp: A, B, C,…
(2) Hoán vị toàn cục: dời từng học sinh về đúng lớp của mình; khi một học sinh vào lớp, một học sinh (ngồi chưa đúng lớp) sẽ phải nhường chỗ.
(3) Sắp xếp cục bộ: cô giáo chủ nhiệm từng lớp sẽ sắp xếp chỗ ngồi cho các em trong lớp của mình.[1]
Cụ thể hơn, với bước Phân lớp dữ liệu ta có thể chia nhỏ thêm các bước như sau (với a[] là mảng cần được sắp xếp có n phần tử):
- Bước 1: Tìm giá trị nhỏ nhất của các phần tử trong mảng(minVal) và vị trí phần tử lớn nhất của các phần tử trong mảng(max).
- Bước 2: Khởi tạo 1 vector L có m phần tử (ứng với m lớp, trong source code lần này chọn số lớp bằng 0.45n).
- Bước 3: Đếm số lượng phần tử các lớp theo quy luật, phần tử a[i] sẽ thuộc lớp k = int((m – 1) * (a[i]-minVal) / (a[max] – minVal)).
- Bước 4: Tính vị trí kết thúc của phân lớp thứ j theo công thức L[j] = L[j] + L[j – 1] (j tăng từ 1 đến m – 1). Sở dĩ như vậy bởi ta có thể hình dung như sau:
.jpg)
Sau khi đã có được vị trí kết thúc của các phân lớp ta tiến hành bước Hoán vị toàn cục.
Việc này sẽ hình thành các chu trình hoán vị: mỗi khi ta đem một phẩn tử ở đâu đó đến một vị trí nào đó thì ta phải nhấc phần tử hiện tại đang chiếm chỗ ra, và tiếp tục với phần tử bị nhấc ra và đưa đến chỗ khác cho đến khi quay lại vị trí ban đầu thì hoàn tất vòng lặp.
- Vấn đề 1: Vậy làm thế nào để khi cầm trong tay 1 phần tử nào đó, ta biết phải bỏ nó vào chỗ nào cho phù hợp? Câu trả lời thật đơn giản, ta tính xem nó phải nằm ở phân lớp nào, rồi bỏ nó vào cái vị trí hiện tại của phân lớp đó, và vì ta bỏ vào phân lớp đó 1 phần tử nên phải lùi vị trí của phân lớp lại 1 đơn vị.
- Vấn đề 2: Mặc dù ta đã đi qua 1 chu trình nhưng vẫn còn những phần tử chưa ở đúng chỗ thì phải làm thế nào? Cũng đơn giản, tiến hành 1 chu trình khác cho đến khi không còn con thỏ nào trong chuồng bò và ngược lại nữa thì thôi.
- Vấn đề 3: Vậy là ta có một số các chu trình cần phải xử lý, vậy tại mỗi chu trình ta phải bắt đầu từ phần tử nào của mảng (Cycle leaders searching)? Đây cũng là một trong những điều đơn giản: ta chỉ việc duyệt từ đầu đến cuối mảng và tìm xem phần tử nào không nằm trong phân lớp (I<L[K[I]]), và bắt đầu bằng phần tử đó.[2]
Source code của bước hoán vị toàn cục có thể biểu diễn như sau:
swap(a[max], a[0]);
int nmove = 0;
int j = 0;
int k = m - 1;
int flash;
while (nmove < n - 1)
{
while (j > L[k] - 1)
{
j++;
k = int(c1*(a[j] - minVal));
}
flash = a[j];
if (k < 0) break;
while (j != L[k])
{
k = int(c1*(flash - minVal));
--L[k];
swap(flash, a[L[k]]);
++nmove;
}
}Một số lưu ý trong đoạn code trên:
- Trước hết chúng ta đổi chỗ a[max] và a[0] bởi chúng ta khởi tạo giá trị k = m – 1 tương ứng với phân lớp mà a[max] thuộc về, do bắt đầu tại phần tử này nên biến j ban đầu cũng được khởi tạo bằng 0.
- Với tối đa n – 1 lần swap, n phần tử trong mảng sẽ về đúng phân lớp của mình.
- Khi j > L[k] – 1 nghĩa là khi đó phần tử a[j] đã nằm đúng vị trí phân lớp của nó do đó ta bỏ qua và tiếp tục tăng j lên để xét các phần tử tiếp theo.
- Như đã nói ở trên cứ mỗi khi đưa 1 phần tử về đúng phân lớp của nó ta lại giảm vị trí cuối cùng của phân lớp đó xuống (đồng thời tăng biến đếm số lần swap lên 1 đơn vị), quá trình này được thực hiện cho tới khi L[k] = j, điều này cũng tương đương với việc phân lớp k đã đầy.
Cuối cùng, sau bước hoán vị toàn cục, mảng của chúng ta hiện tại sẽ được chia thành các lớp(thứ tự các phần tử trong lớp vẫn chưa đúng) do đó để đạt được trạng thái đúng thứ tự thì khoảng cách phải di chuyển của các phần tử là không lớn vì vậy Insertion Sort sẽ là thuật toán thích hợp nhất để sắp xếp lại mảng có trạng thái như vậy.
(Về source code của các thuật toán sắp xếp các bạn có thể xem ở đây: GitHub – HaiDuc0147/sortingAlgorithm)
Dưới đây là demo cách chạy thuật toán với 1 mảng có 7 phần tử:
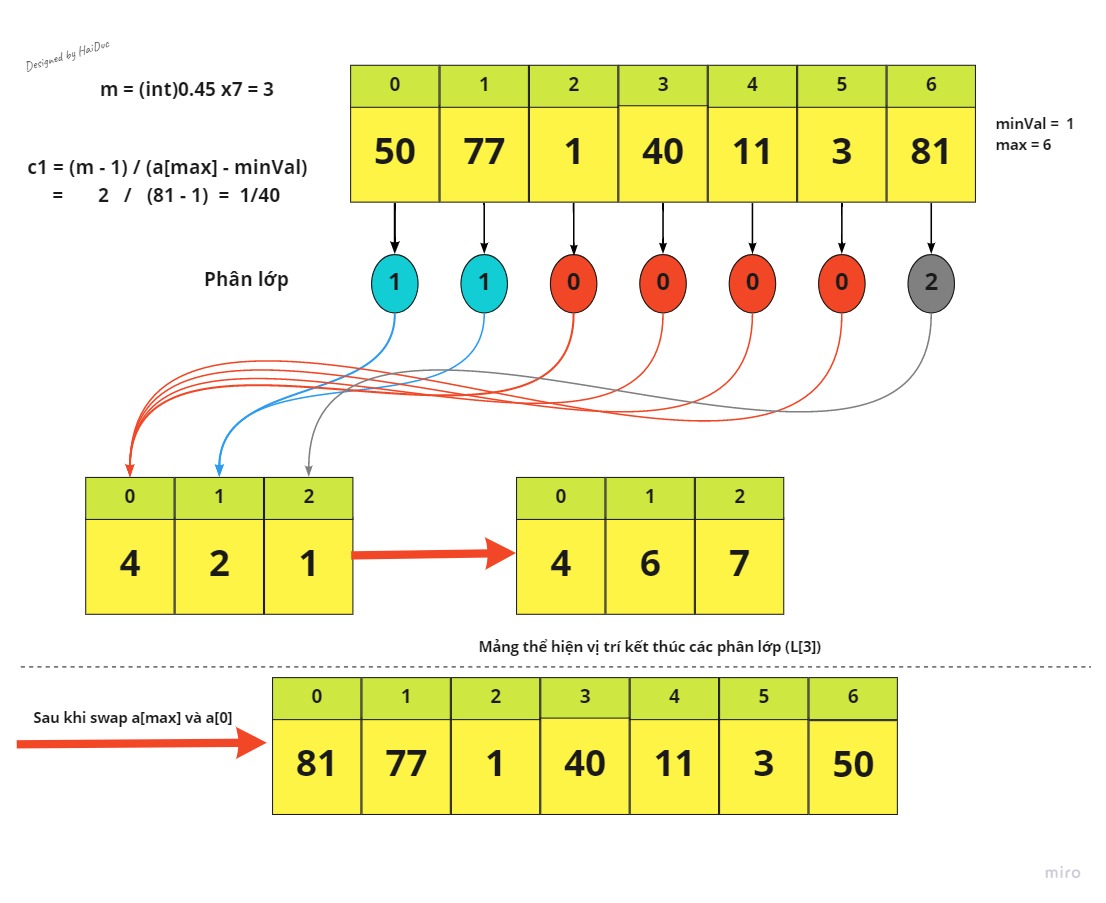
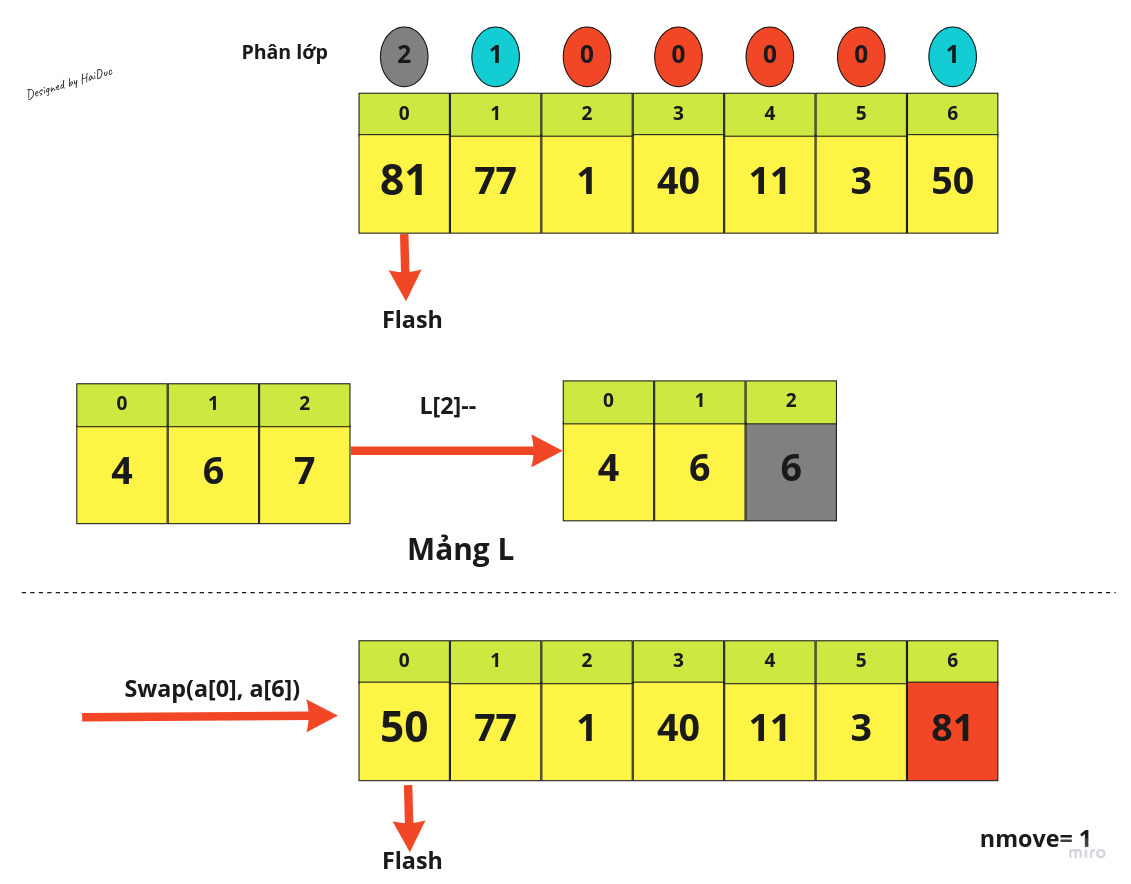
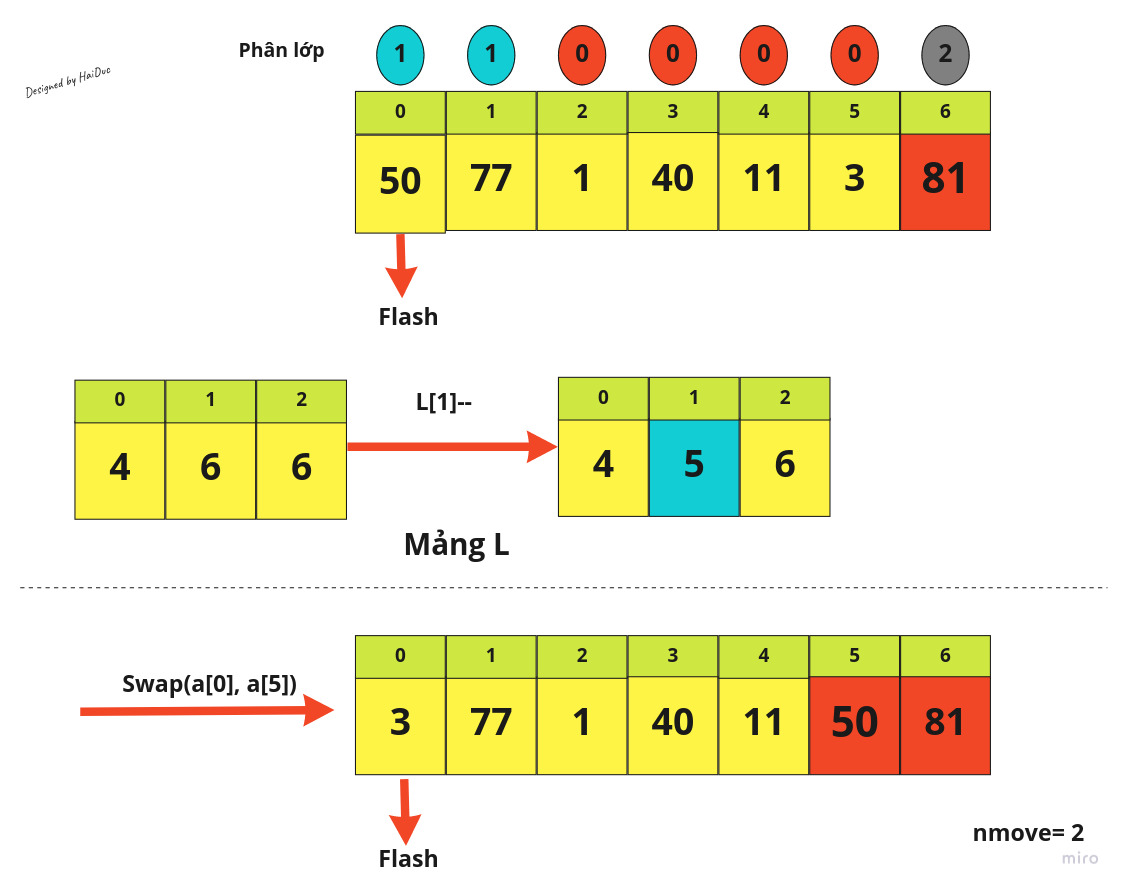
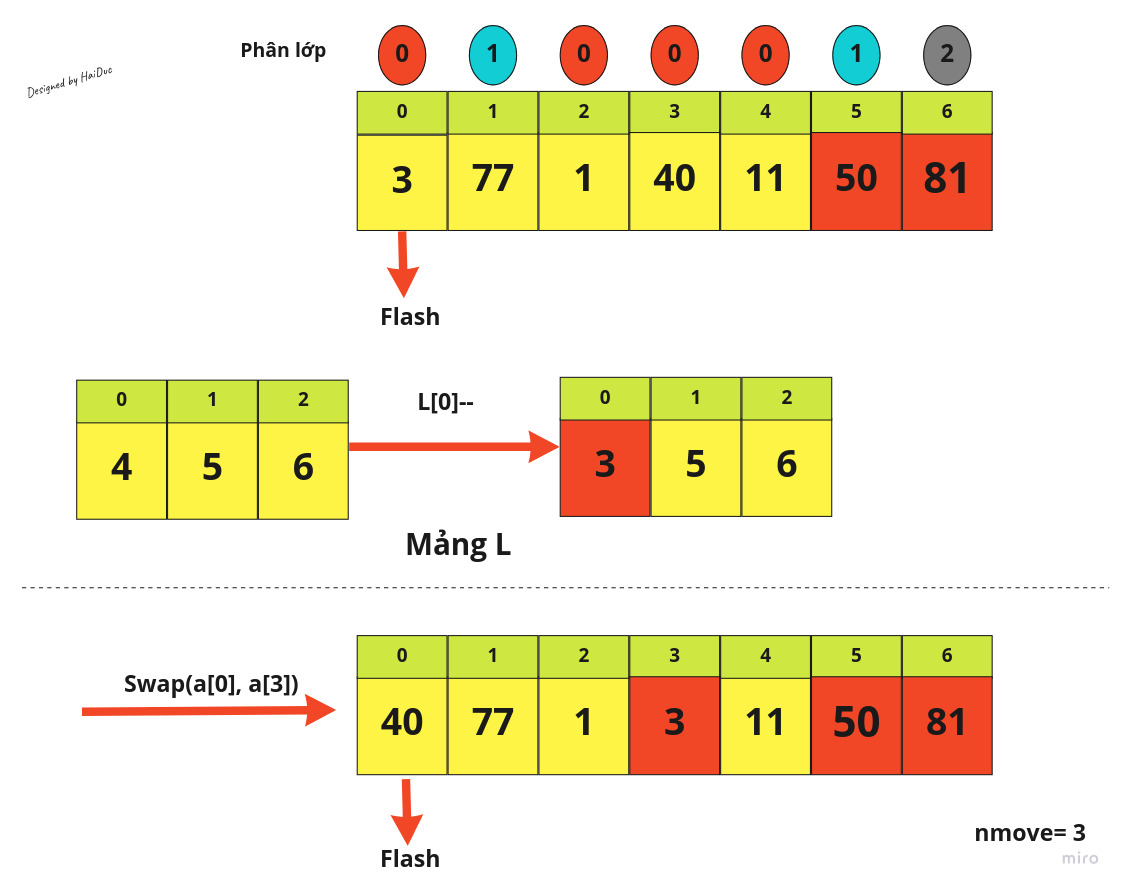
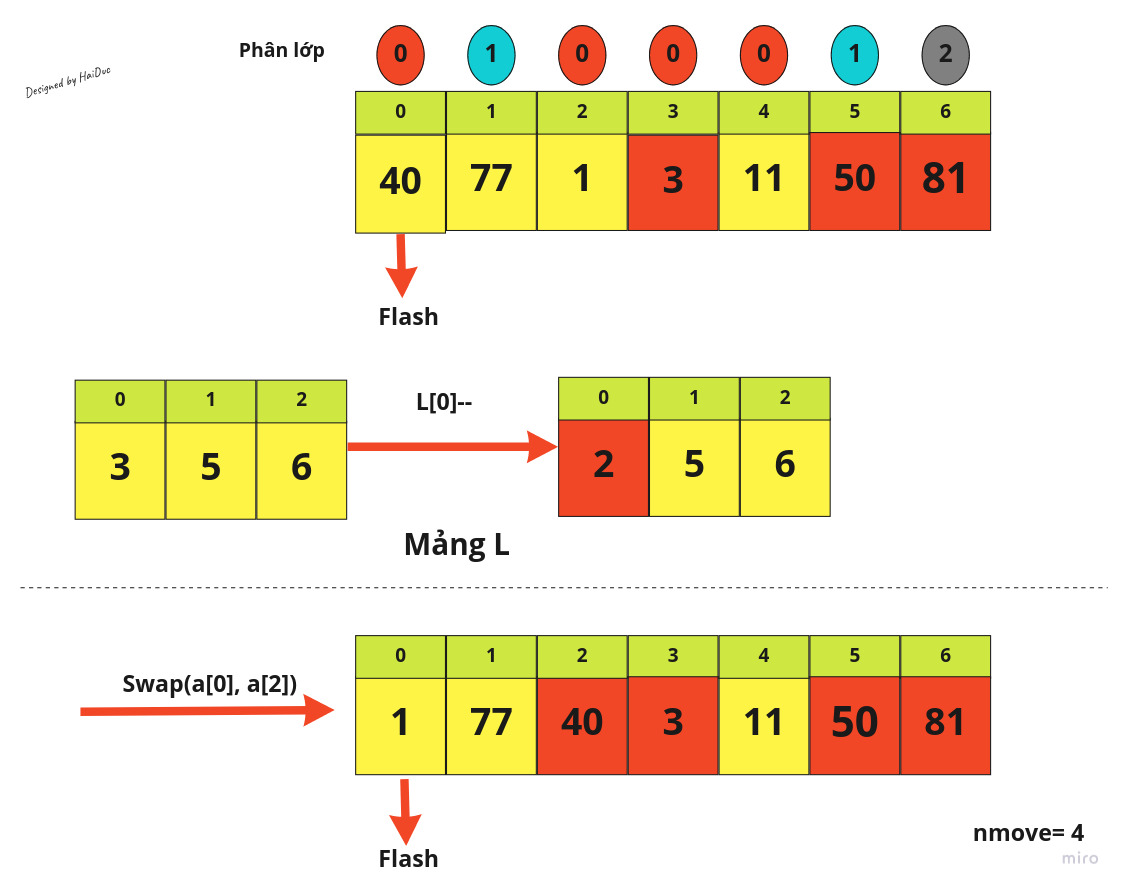
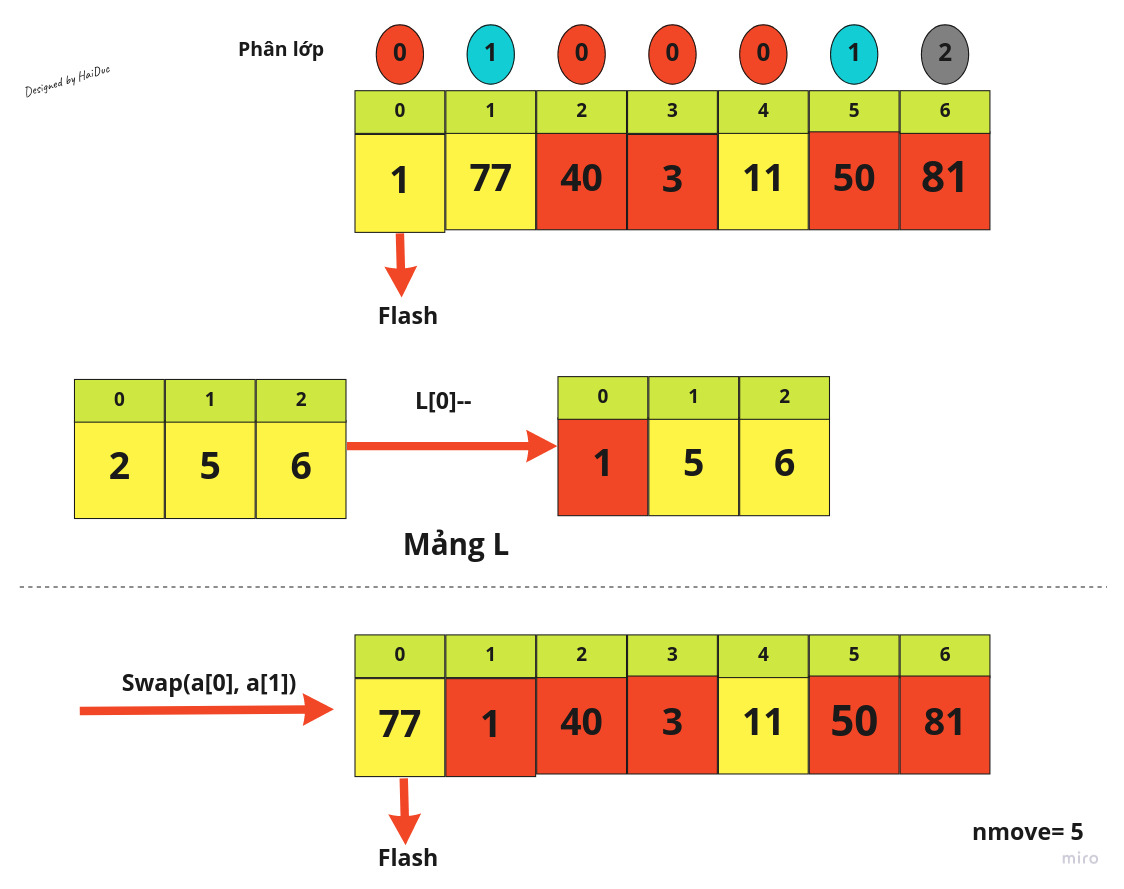
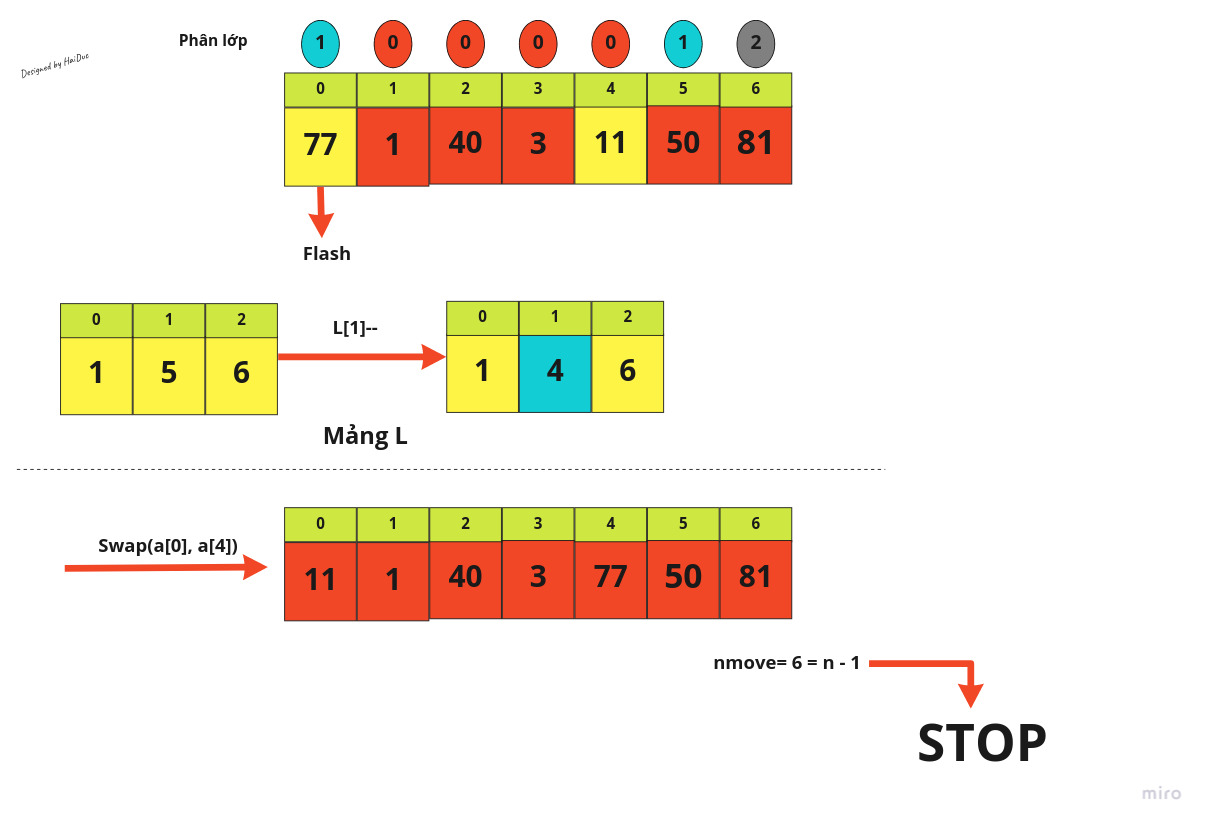
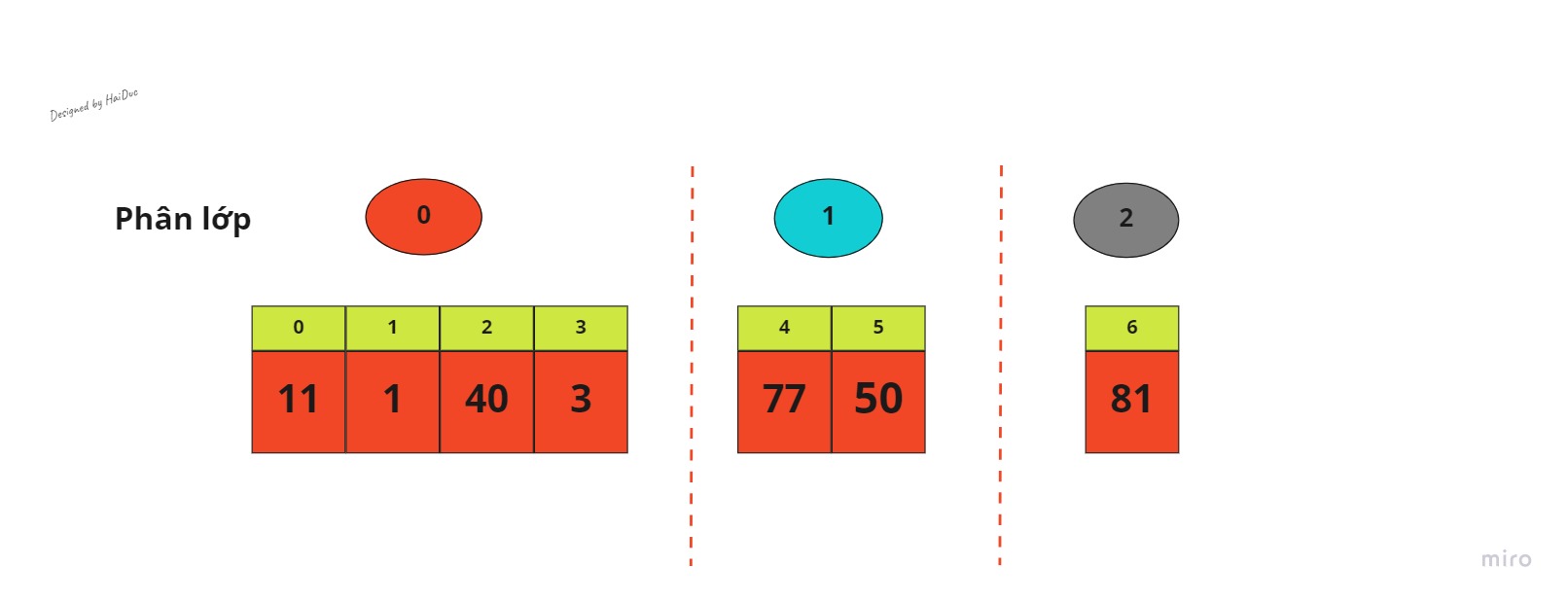
Đến đây, các phần tử của mảng sẽ về đúng với phân lớp của mình, do đó theo phân tích ở trên, ta dùng Insertion Sort để sắp xếp lại mảng này.
Tạm kết
Cảm ơn các bạn đã dành thời gian đọc bài viết. Hi vọng những chia sẻ của mình có thể giúp các bạn biết được thêm 1 thuật toán hay trong vô vàn các thuật toán sắp xếp. Hẹn gặp lại các bạn trong các bài viết sau!
Tài liệu tham khảo:
[2]https://www.ddth.com/archive/index.php/t-64851.html
https://www.neubert.net/FSOIntro.html
Hình ảnh sử dụng trong bài viết:
wp6070488.jpg (4800×2700) (wallpapercave.com)
15br-theflash-screenshot-newsheader-1920×1080-0e77cc2ff454.jpg (1920×1080) (unrealengine.com)







Post Comment