
Chương Trình Đệ Quy Hoạt Động Như Thế Nào?
Bài viết sẽ trình bày về khái niệm đệ quy, cấu trúc của một chương trình đệ quy, cách máy tính thực thi chương trình đệ quy như thế nào
1. Đệ quy là gì?
Thử tìm kiếm từ khóa “recursion” (hay “đệ quy”) trên Google thử nhé! Kết quả bạn thu được như sau: 
Có thể lần đầu tiên khi thấy dòng chữ “Có phải bạn muốn tìm” bạn sẽ suy nghĩ rằng mình đã gõ sai chính tả đâu đó, bạn click vào từ khóa “recursion” mà Google đề xuất. Nhưng kết quả bạn thu được vẫn thế, dòng chữ “Có phải bạn muốn tìm” vẫn tiếp tục hiện ra. Thực ra đây cũng là một ví dụ của đệ quy. Đệ quy xảy ra khi một sự vật được định nghĩa theo chính nó hoặc thuộc loại của nó. Ví dụ chúng ta có thể định nghĩa số tự nhiên như sau:
- 0 là số tự nhiên.
- n là số tự nhiên nếu (n-1) là số tự nhiên.
Trong định nghĩa trên ta thấy rằng trong định nghĩa số tự nhiên lại dùng định nghĩa số tự nhiên, đây chính là đệ quy. Trong lập trình, đệ quy có nghĩa là hàm gọi lại chính nó trong thân hàm.
void Recursion()
{
....
Recursion();
....
}2. Cấu trúc một chương trình đệ quy
Một chương trình đệ quy thông thường sẽ có cấu trúc như sau:
{
if(điều kiện dừng đệ quy) // phần cơ sở
// Làm gì đó
else
{
....
// Thực hiện gọi đệ quy
....
}
}
Một ví dụ của đệ quy là việc tính giai thừa bởi lẽ trong định nghĩa của giai thừa cũng có chứa yếu tố đệ quy:
- 0! = 1! = 1
- n! = n*(n-1)!
Code của hàm tính giai thừa có thể được viết như sau:
int fact(int n)
{
if (n == 0 || n == 1)
return 1;
return n * fact(n - 1);
}Qua ví dụ trên ta có thể thấy rằng một trong những ưu điểm của đệ quy đó là code rất dễ hiểu cho người đọc vì nó rất sát với công thức truy hồi mà chúng ta tìm ra. Sơ đồ gọi hàm với n = 5 có thể được diễn tả như hình sau:
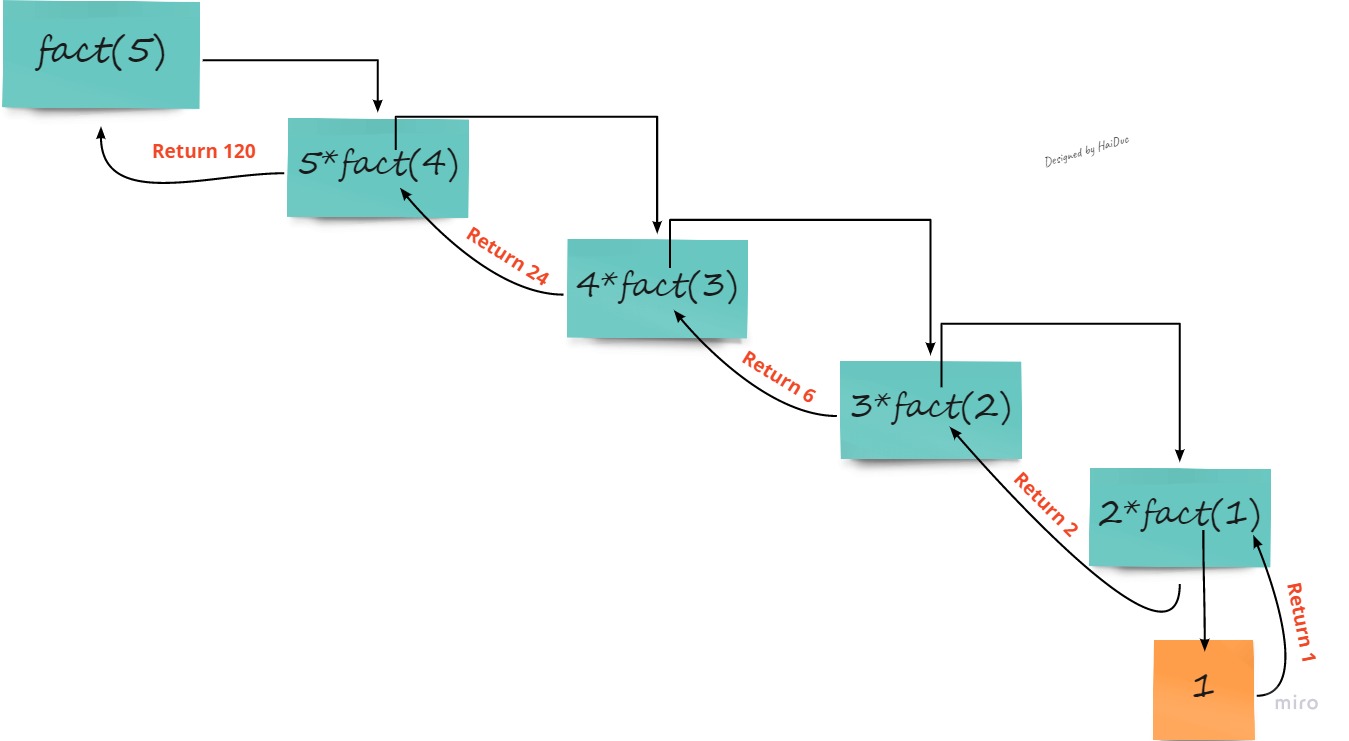
3. Một chương trình đệ quy sẽ hoạt động như thế nào?
Đây là ý mà mình muốn nhấn mạnh trong bài viết lần này. Một trong những câu nói đùa của dân lập trình viên với nhau đó là muốn hiểu đệ quy là gì trước hết phải hiểu đệ quy là gì,… Tuy nhiên, theo mình muốn hiểu được cơ chế hoạt động của chương trình đệ quy ta cần phải hiểu được luồng chạy và cơ chế lưu stack của chương trình, chương trình đệ quy sẽ kết thúc quá trình hoạt động của nó khi không còn câu lệnh nào được thực hiện và stack đã rỗng. Nói về stack thì sau lệnh gọi đệ quy, các câu lệnh chưa được thực thi dưới đó sẽ được lưu vào stack (theo nguyên tắc LIFO – Last In First Out) với các giá trị biến và tham số hiện hành. Bên cạnh đó, có 3 câu hỏi mà mình nghĩ các bạn nên suy nghĩ trước khi sử dụng đệ quy cho một vấn đề, đó là:
- Phần cơ sở (base case) của chương trình là gì?
- Phần đệ quy của chương trình là gì?
- Với phần đệ quy như vậy liệu trong quá trình thực thi chương trình có đạt được về phần cơ sở để giải quyết vấn đề hay không? Bởi nếu không chương trình sẽ gặp hiện tượng tràn stack (stack overflow).
Một trong những bài toán kinh điển có thể được giải quyết bởi đệ quy là bài toán tháp Hà Nội.
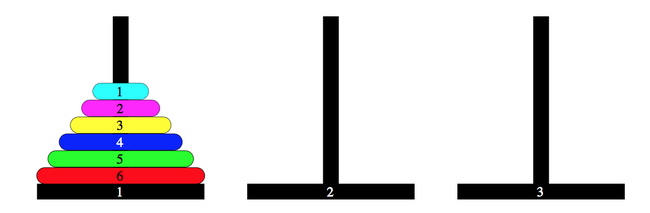
(Link ảnh: https://genk.mediacdn.vn/2017/photo-1-1488855314632.png)
Giả thiết đề bài là có n đĩa ở cột 1(các đĩa từ dưới lên trên được xếp theo quy tắc từ lớn đến nhỏ) cần chuyển hết sang cột 2 với các quy tắc sau:
- Mỗi lần chỉ được di chuyển 1 đĩa.
- Các đĩa lớn không được đặt trên các đĩa nhỏ.
- Có thể dùng cột 3 làm cột trung gian trong quá trình chuyển đĩa.
Ý tưởng của bài toán như sau:
- Nếu chỉ có 1 đĩa ở cột 1 ta chỉ đơn giản là chuyển đĩa đó từ cột 1 sang cột 2 (base case).
- Nếu số đĩa lớn hơn 1 việc ta cần làm chia ra 3 bước như sau:
- Chuyển n – 1 đĩa từ cột 1 sang cột 3, lấy cột 2 làm trung gian (phần đệ quy).
- Chuyển 1 đĩa từ cột 1 sang cột 2.
- Chuyển n – 1 đĩa từ cột 3 sang cột 2, lấy cột 1 làm trung gian (phần đệ quy).
Đoạn code giải quyết vấn đề trên có thể được viết như sau:
void HaNoiTower(int n, int a, int b, int c)
{
if (n == 1)
cout << a << " ----> " << b << endl;
else
{
HaNoiTower(n - 1, a, c, b); // Chuyển n - 1 đĩa từ a -> c
cout << a << " ----> " << b << endl; // Chuyến 1 đĩa từ a -> b
HaNoiTower(n - 1, c, b, a); // Chuyển n - 1 đĩa từ c -> b
}
}Ở đây, một lần nữa chúng ta thấy được ưu điểm khi cài đặt giải thuật đệ quy đó là code sẽ sát với phần ý tưởng đã đề ra ban đầu. Tuy nhiên, câu hỏi đặt ra là với giải thuật như vậy thì khi thực thi chương trình, máy tính sẽ thực thi như thế nào? Một trong những cách để trả lời câu hỏi trên đó là thử chạy tay đoạn chương trình này. Ở đây, để demo thì mình sẽ thử chạy tay với n = 3.
.jpg)
-1.jpg)
Để hiểu rõ hơn về cơ chế lưu stack thì hãy xét tiếp ví dụ 2 hàm printArray sau:
/*Cách 1*/
void printArray1(int a[], int n)
{
if (n == 0)
return;
else
{
printArray1(a, n - 1);
cout << a[n - 1] << " ";
}
}
/*Cách 2*/
void printArray2(int a[], int n)
{
if (n == 0)
return;
else
{
cout << a[n - 1] << " ";
printArray2(a, n - 1);
}
int main()
{
int a[10] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
printArray1(a, 10);
printArray2(a, 10);
system("pause");
return 0;
}Thử chạy chương trình trên, nhìn sự khác biệt kết quả đầu ra của 2 hàm và giải thích vì sao lại có sự khác nhau đó nhé!
4. Tạm kết
Đệ quy là một công cụ rất mạnh để giải quyết những vấn đề có thể chia nhỏ ra để giải quyết mà trong đó vấn đề được chia nhỏ ra có thể được giải quyết đơn giản hơn vấn đề ban đầu. Tuy nhiên, đây là một khái niệm tương đối khó hiểu với những người mới tiếp xúc với lập trình. Hi vọng với những chia sẻ của mình trên đây có thể giúp các bạn hiểu rõ hơn về vấn đề này. Chúc các bạn học tốt!







Post Comment