[tree] number Of Path

Cho một đồ thị dạng cây n đỉnh được đánh số từ 1 tới n, gốc của đồ thị là đỉnh 1. Một đỉnh được gọi là đỉnh lá khi đỉnh đó chỉ nối với duy nhất 1 đỉnh khác. Bạn hãy viết hàm xác định số đỉnh lá mà đỉnh gốc có thể đi tới được và trên đường đi này không có quá k đỉnh đặc biệt liên tiếp biết:

Các đỉnh đặc biệt được biểu diễn dưới ma trận 1 chiều specialVertices.

Các cạnh của đồ thị được biểu diễn dưới ma trận 2 chiều edges.

Ví dụ

• Cho n = 4, edges = [[1, 2],[1, 3],[1, 4]], specialVertices=[1,3], k = 1, output là numberOfPath(n, edges, specialVertices, k) = 2.
  Giải thích:
  Đồ thị sẽ có dạng như sau: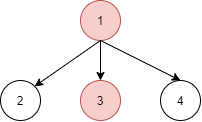
  
  Các đỉnh bôi đỏ là các đỉnh đặc biệt, có thể đi từ đỉnh 1 tới các đỉnh đỉnh lá 2 và 4. Nếu đỉnh 1 không phải đỉnh đặc biệt thì còn có thể đi tới đỉnh 3. 
• Cho n = 7, edges = [[1, 2],[1, 3],[2, 4], [2, 5], [3, 6], [3, 7]], specialVertices=[1,3,5], k = 1, output là numberOfPath(n, edges, specialVertices, k) = 2.
  Giải thích: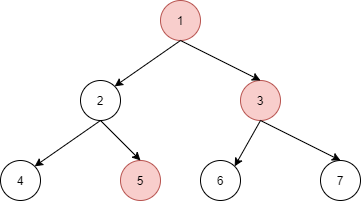
  
  Chỉ có thể đi tới đỉnh 4 và 5.

Đầu vào/Đầu ra

• [Giới hạn thời gian chạy] 0.5s với C++, 3s với Java và C#, 4s với Python, JS và Go

• [Đầu vào] Integer n
  1 <= n <= 1000

• [Đầu vào] Matrix of integers edges.
  edges.size = n - 1
1 <= edges[i][j] <= n

• [Đầu vào] Array of integers specialVertices
  0 <= specialVertices.size <= n
1 <= specialVertices[i] <= n
• [Đầu vào] Integer k
  1 <= k <= n

• [Đầu ra] Integer