[tree] lca

Cho một đồ thị dạng cây n đỉnh (đồ thị dạng cây là đồ thị liên thông có n đỉnh và n - 1 cạnh) và 2 đỉnh u, v. Các đỉnh trong đồ thị được đánh số từ 1 tới n, các cạnh được biểu diễn bằng ma trận 2 chiều edges. Bạn hãy viết hàm xác định đỉnh xa đỉnh gốc nhất mà đi từ đỉnh gốc tới đỉnh u và v đều phải đi qua đỉnh này biết đỉnh gốc là đỉnh 1.

Hình ảnh về đồ thị dạng cây:

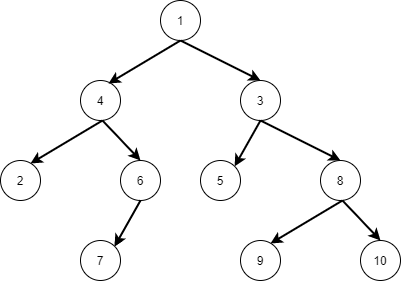
Ví dụ:

• Cho n = 8, edges = [[1, 4], [1, 3], [4, 2], [4, 6], [6, 7], [3, 5], [3, 8]], u = 2, v = 7, output là LCA(n, edges, u, v) = 4.
  Giải thích:
  Đồ thị sẽ có dạng như sau: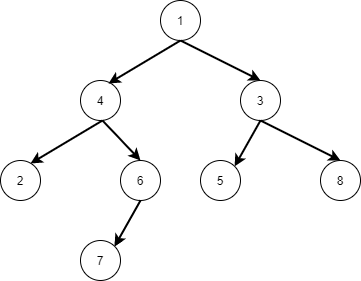
  
  Có thể thấy đỉnh 4 là đỉnh xa đỉnh 1 nhất và từ đỉnh 1 đi tới đỉnh 2 và 7 luôn phải đi qua đỉnh 4.
• Cũng với đồ thị trên nếu u = 3, v = 5, output là LCA(n, edges, u, v) = 3.
• Cũng với đồ thị trên nếu u = 2, v = 8, output là LCA(n, edges, u, v) = 1.

Đầu vào/Đầu ra

• [Giới hạn thời gian chạy] 0.5s với C++, 3s với Java và C#, 4s với Python, JS và Go

• [Đầu vào] Integer n
  1 <= n <= 1000

• [Đầu vào] Matrix of integer edges.
  edges.size = n - 1
1 <= edges[i][j] <= n

• [Đầu vào] Integer u
  1 <= u <= n
• [Đầu vào] Integer v
  1 <= v <= n

• [Đầu ra] Integer