Is Rectangle

Bạn được cho 4 điểm trên mặt phẳng hai chiều: points = [[x1, y1], [x2, y2], [x3, y3], [x4, y4]].

Bạn nối các điểm đó theo thứ tự đã cho, và nối điểm thứ 4 ngược về điểm đầu tiên.

Viết chương trình kiểm tra xem hình được tạo bởi cách nối các điểm đã cho theo thứ tự có tạo thành hình chữ nhật hay không?

Ví dụ

• Với points = [[0, 0], [2, 0], [2, 1], [0, 1]], thì kết quả isRectangle(points) = true.
  Hình dưới đây là một hình chữ nhật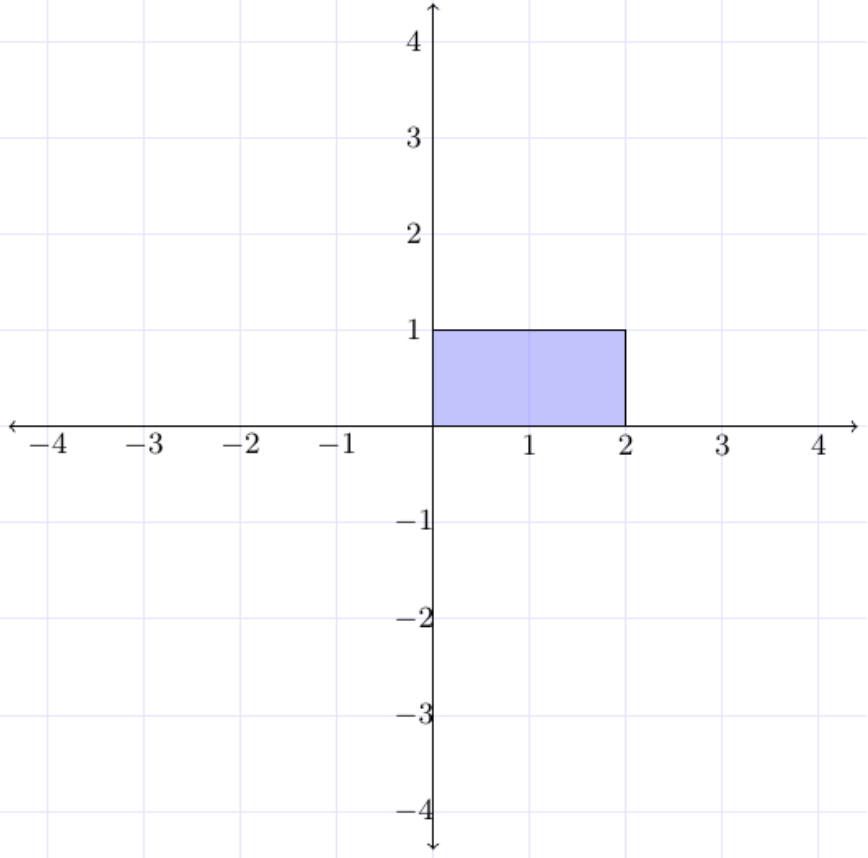
  

• Với points = [[0, 0], [2, 1], [2, 0], [0, 1]], thì kết quả isRectangle(points) = false.
  Hình bên dưới không phải là một hình chữ nhật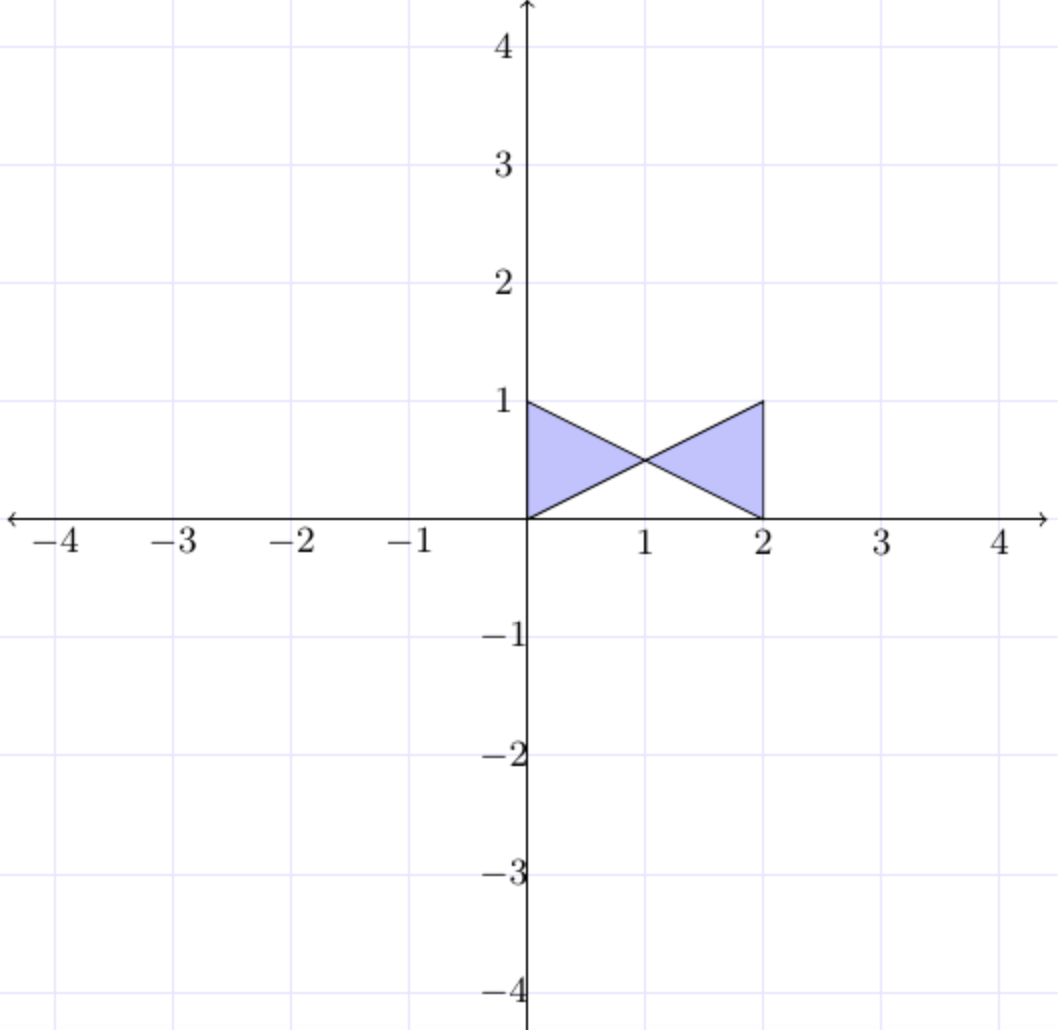
  

• Với points = [[0, 0], [1, 1], [0, 2], [-1, 1]], thì kết quả isRectangle(points) = true.
  Hình bên dưới là một hình vuông (dạng đặc biệt của hình chữ nhật), mặc dù các cạnh của nó không song song với trục tọa độ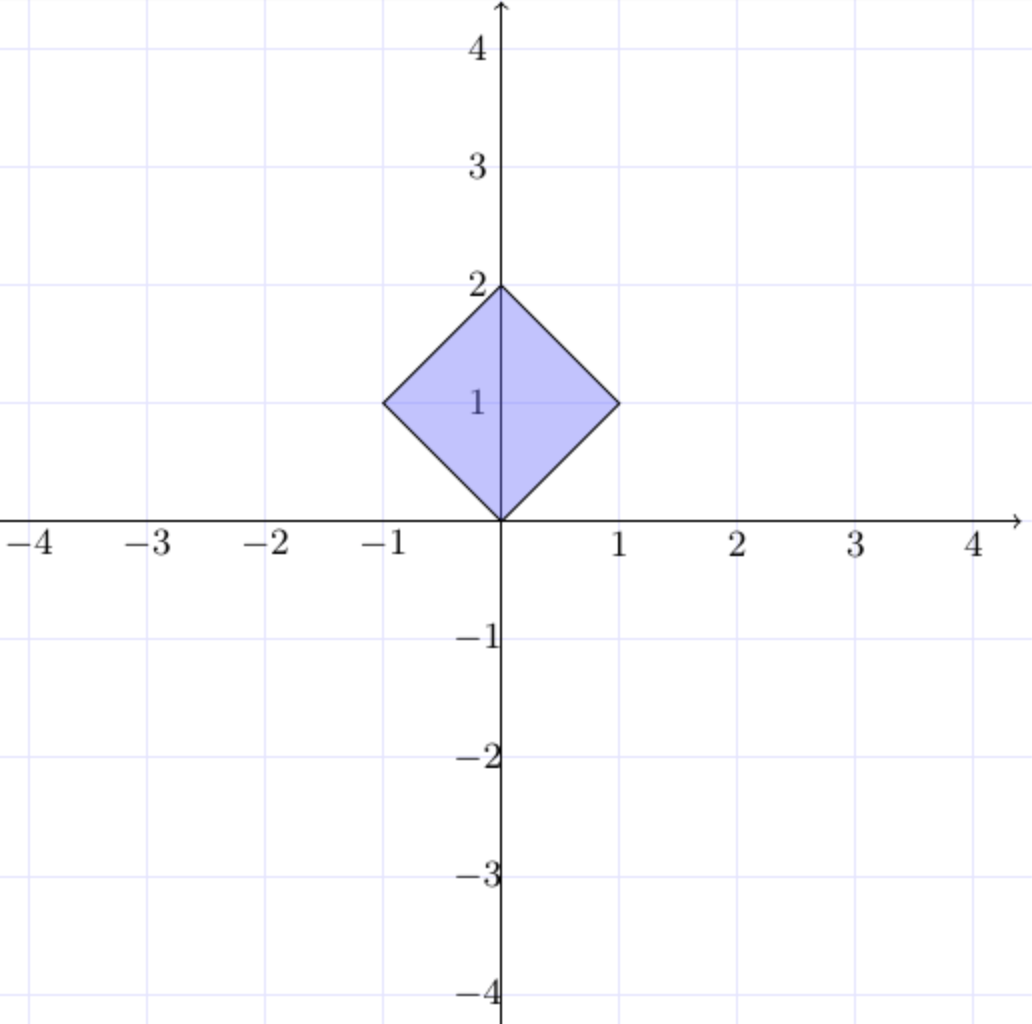
  
  

Đầu vào/Đầu ra

• [Thời gian chạy] 0.5 giây

• [Đầu vào] array.array.integer points

  Tọa độ các điểm đầu vào theo định dạng [[x1, y1], [x2, y2], [x3, y3], [x4, y4]].

  Điều kiện:
  points.length == 4,
  points[i].length == 2,
  points[i] ≠ points[j], i ≠ j,
  -10 ≤ points[i][j] ≤ 10.

• [Đầu ra] boolean

  true nếu 4 điểm được cho theo thứ tự tạo thành hình chữ nhật, ngược lại trả về false.

Lý thuyết 

• 2 vector u(xU, yU) và v(xV, yV) vuông góc với nhau khi và chỉ khi u * v = 0, tức là xU * xV + yU * yV = 0

bool isPerpen(vector <int> U, vector <int> V) {
    return U[0] * V[0] + U[1] * V[1] == 0;
}

• Hình chữ nhật là hình có 4 góc đều vuông, tức là với 3 đỉnh liên tiếp A, B, C thì vector AB và vector BC luôn vuông góc với nhau.

Hướng dẫn bài tập.

Code mẫu:

Ngôn ngữ Java:

	boolean isRectangle(int[][] points) {
		List<Double> lst = new ArrayList<>();
		lst.add(distanceTwoPoin(points[0][0], points[0][1], points[1][0], points[1][1]));
		lst.add(distanceTwoPoin(points[2][0], points[2][1], points[3][0], points[3][1]));
		lst.add(distanceTwoPoin(points[3][0], points[3][1], points[0][0], points[0][1]));
		lst.add(distanceTwoPoin(points[1][0], points[1][1], points[2][0], points[2][1]));
		lst.add(distanceTwoPoin(points[0][0], points[0][1], points[2][0], points[2][1]));
		lst.add(Math.sqrt(((Math.pow(lst.get(0), 2) + Math.pow(lst.get(2), 2)))));

		for (int i = 0; i < lst.size(); i = i + 2) {
			if (Double.compare(lst.get(i), lst.get(i + 1)) != 0) {
				return false;
			}
		}

		return true;
	}

	double distanceTwoPoin(int xpoint1, int ypoint1, int xpoint2, int ypoint2) {
		double height = Math.abs(xpoint1 - xpoint2);
		double weight = Math.abs(ypoint1 - ypoint2);
		return Math.sqrt(((Math.pow(height, 2) + Math.pow(weight, 2))));
	}