Find Square Side

Cho 4 đỉnh của 1 hình vuông không theo thứ tự

Hãy tính diện tích của hình vuông (bình phương của một cạnh).

Ví dụ:

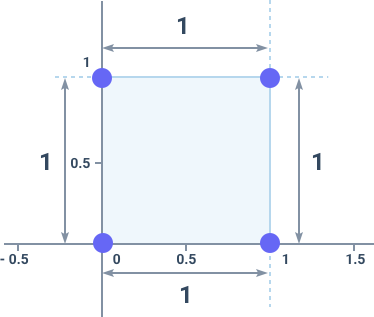
• Với x = [0, 1, 0, 1] và y = [0, 1, 1, 0], kết quả findSquareSide(x, y) = 1.
  
  Xem hình dưới để hiểu rõ hơn:

Đầu vào/Đầu ra

• [Thời gian chạy] 0.5 giây

• [Đầu vào] array.integer x, y

  Mảng 4 phần tử thể hiện tọa độ 4 đỉnh của hình vuông

• [Đầu ra] integer

  Diện tích hình vuông.

Lý thuyết :

• Khi xử lí các bài toán hình học, các bạn sẽ thường xuyên phải làm việc với các điểm, và các mối quan hệ giữa chúng
• Có 2 hệ tọa độ thường được sử dụng, là tọa độ Descartes (Oxy) và tọa độ ô vuông trên bảng
• Với hệ Oxy :
  • Các điểm sẽ là các chấm nhỏ, nằm trên mặt phẳng 2 chiều
  • Hình ảnh minh họa :
  • Cho 2 điểm (x1, y1) và (x2, y2), thì
    • Vector u tạo bởi 2 điểm : (x2 - x1, y2 - y1)
    • Khoảng cách dist giữa 2 điểm : √( (x2 - x1)² + (y2 - y1)² )
    • Giả sử x1 <= x2, y1 <= y2, diện tích S của hình chữ nhật tạo bởi 2 đỉnh đối (x1, y1) và (x2, y2) : (x2 - x1) * (y2 - y1)
• Với hệ ô vuông :
  • Các điểm là các ô vuông con 1 * 1, nằm trong 1 bảng chữ nhật
  • Hình ảnh minh họa :
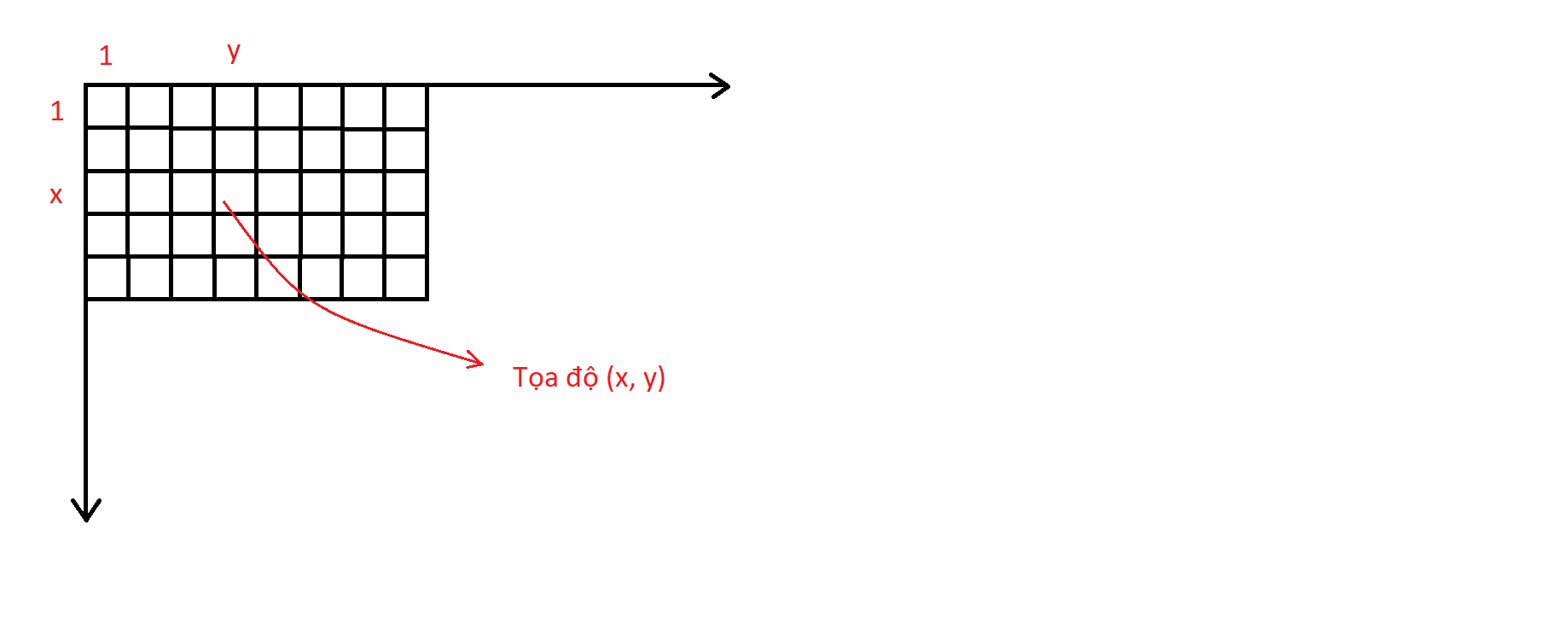
  • Cho 2 điểm (x1, y1) và (x2, y2), thì
    • Giả sử x1 <= x2, y1 <= y2, diện tích S của hình chữ nhật tạo bởi 2 đỉnh đối (x1, y1) và (x2, y2) : (x2 - x1 + 1) * (y2 - y1 + 1)

Hướng dẫn bài tập.

Code mẫu:

Ngôn ngữ Java:

int findSquareSide(int[] x, int[] y) {
		double c1, c2, c;
		c1 = Math.pow(x[1] - x[0], 2);
		c2 = Math.pow(y[1] - y[0], 2);
		c = ((c1 + c2));

		double c12, c22, c3;
		c12 = Math.pow(x[2] - x[0], 2);
		c22 = Math.pow(y[2] - y[0], 2);
		c3 = ((c12 + c22));

		double c122, c222, c32;
		c122 = Math.pow(x[3] - x[0], 2);
		c222 = Math.pow(y[3] - y[0], 2);
		c32 = ((c122 + c222));

		if (c == c3) {
			return (int) c;
		} else {
			return (int) c32;
		}

	}